本博客源自我的洛谷博客<https://www.luogu.com.cn/article/kcvvk8bl> (现在改成专栏了),写作时间 2021-06-28 22:29
根据OI wiki学习
一个指针党的学习笔记
1. 旋转Treap:
OI wiki 上对旋转 Treap 的介绍甚少,不过根据 Treap 的性质及 Splay 里对旋转的介绍,做出来并不难。
Treap 其实就是一个 普通二叉搜索树 与 堆 的合体,旋转Treap通过旋转(代替堆里面的swap)维持堆的性质。
OI wiki 上有个tip ,但是我要写的是Treap啦?
请读者尝试自行模拟 $6$ 种旋转情况,以理解 Splay 的基本思想。
旋转是 旋转Treap 和 Splay 的核心,大概模拟一下(一种,其他五种同理): 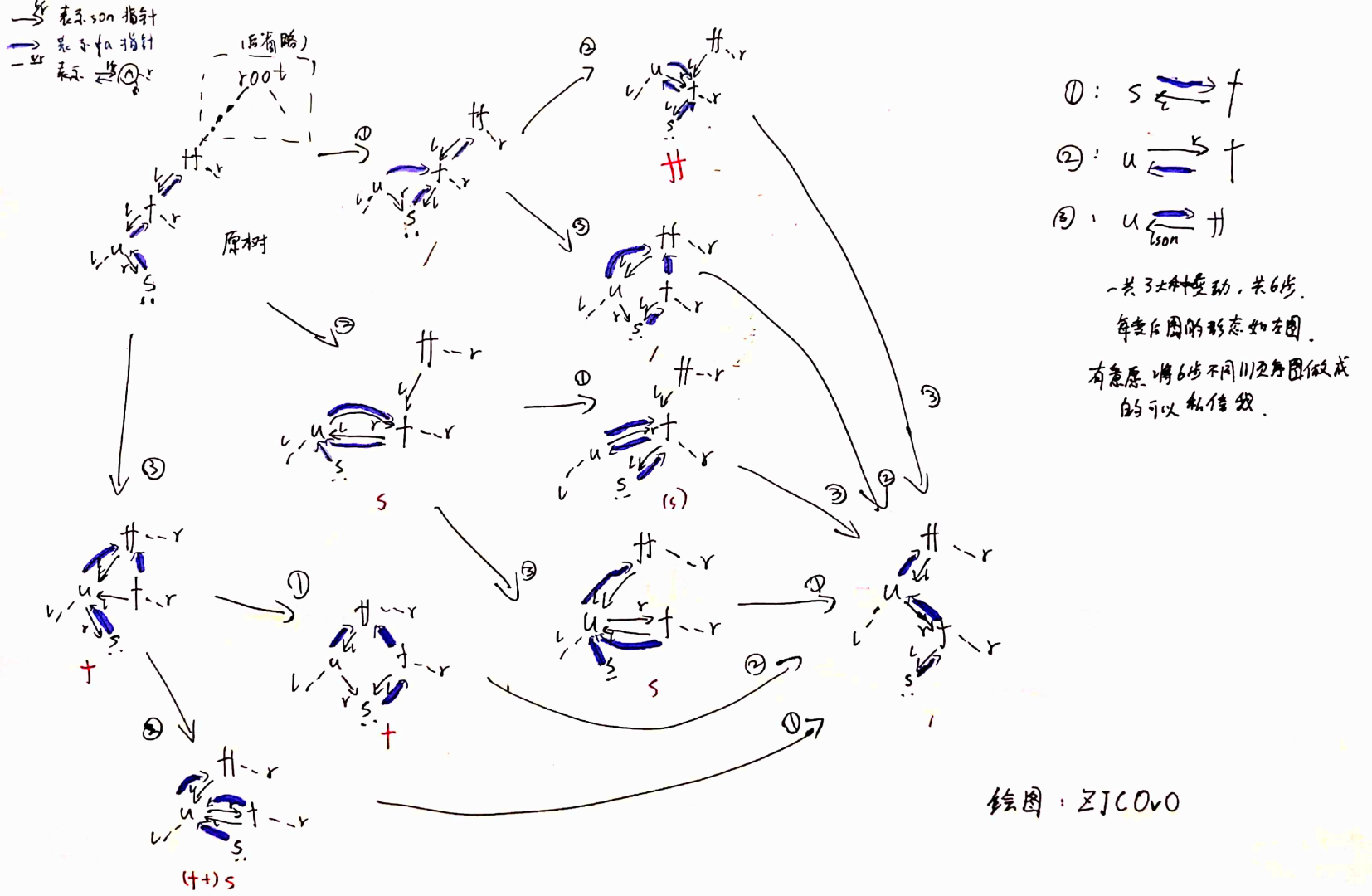
一次旋转分为六步,我将之总结为三大步(如图):
f<-su<-fff<-u
OI wiki 上的那份代码三次操作顺序为 1-2-3 所以必须在函数里新建 ff 指针/变量
其实什么顺序都无所谓啦,只要理清逻辑就好了,记得存一下相关变量。
我的代码(指针版的呢,略微有点压行):
void rot(Treap *u){
bool dir=(u==u->fa->son[1]);Treap *ff=u->fa->fa; //store related varibles
u->fa->son[dir]=u->son[!dir]; //step 1
if(u->son[!dir]) u->son[!dir]->fa=u->fa;
u->son[!dir]=u->fa; u->fa->fa=u; //step 2
if(ff) ff->son[u->fa==ff->son[1]]=u; //step 3
u->fa=ff;
//maintain ...
}修改操作里旋转Treap的写法感觉和堆类似,只不过维护堆性质的swap要改为rot。
加一个点就先按照BST的规则把新点在叶子创立,向上维护堆的性质。
删一个点就先将它的优先级设最低,向下维护堆的性质,当这个点成为叶子时就可以放心的把它删掉了。(实操中不用改优先级,也不必等它成为叶子,具体见代码)
查询操作如一个常规的BST。
上代码~
平衡树(splay)代码
#include<ctime>
#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
struct Treap{
int cnt,val,pri,sz;Treap *son[2],*fa;
}pool[500005],*rt=&pool[0],*bdN=rt;
#define mt(x) x->sz=(x->son[0]?x->son[0]->sz:0)+(x->son[1]?x->son[1]->sz:0)+x->cnt
void rot(Treap *u){
bool dir=(u==u->fa->son[1]);Treap *ff=u->fa->fa;
u->fa->son[dir]=u->son[!dir]; //step 1
if(u->son[!dir]) u->son[!dir]->fa=u->fa;
u->son[!dir]=u->fa; u->fa->fa=u; //step 2
if(ff) ff->son[u->fa==ff->son[1]]=u; //step 3
u->fa=ff;mt(u->son[!dir]);mt(u);
while(rt->fa)rt=rt->fa;
}
inline void ins(int x){
Treap *p=rt;
while(p->cnt!=0){
p->sz++;if(x==p->val){p->cnt++;return;}
if(!p->son[x>p->val])p->son[x>p->val]=++bdN,bdN->fa=p;
p=p->son[x>p->val];
}
p->val=x;p->cnt++;p->sz++;p->pri=rand();
while(p->fa&&p->pri>p->fa->pri) rot(p);
}
inline bool del(int x){
#define mttr while(p){p->sz--;p=p->fa;} //maintain to root
Treap *p=rt;
while(p&&p->cnt!=0){
if(x==p->val)break;
if(!p->son[x>p->val])return 0;
p=p->son[x>p->val];
}if(!p||p->cnt==0) return 0;
if(p->cnt>1){p->cnt--;mttr return 1;}
while(p->son[0]&&p->son[1]){rot(p->son[p->son[0]->pri<p->son[1]->pri]);}
if(p->son[0]) p->son[0]->fa=p->fa;
if(p->son[1]) p->son[1]->fa=p->fa;
if(p->fa) p->fa->son[p==p->fa->son[1]]=(p->son[0])?p->son[0]:p->son[1];
else{
if(p->son[0])rt=p->son[0];
else if(p->son[1])rt=p->son[1];
else rt=++bdN;
}
p=p->fa;mttr return 1;
}
int rk(int x){
int ans=0;Treap *p=rt;
while(p&&p->cnt!=0){
if(x<p->val)p=p->son[0];
else if(x==p->val){ans+=(p->son[0]?p->son[0]->sz:0);ans++;return ans;}
else ans+=(p->son[0]?p->son[0]->sz:0)+p->cnt,p=p->son[1];
} return ans;
}
Treap *loc(int x){
Treap *p=rt;
while(p&&p->cnt!=0){
if(x==p->val)return p;
if(!p->son[x>p->val])return NULL;
p=p->son[x>p->val];
}return NULL;
}
Treap *pre(int x){
Treap *p=rt;
while(p&&p->cnt!=0){
if(x==p->val)break;
if(!p->son[x>p->val]){if(x>p->val)return p;break;}
p=p->son[x>p->val];
}if(!p)return NULL;
if(p->son[0]){p=p->son[0];while(p->son[1])p=p->son[1];return p;}
while(p->fa&&p->fa->son[0]==p) p=p->fa;
return p->fa;
}
Treap *nxt(int x){
Treap *p=rt;
while(p&&p->cnt!=0){
if(x==p->val)break;
if(!p->son[x>p->val]){if(x<p->val)return p;break;}
p=p->son[x>p->val];
}if(!p)return NULL;
if(p->son[1]){p=p->son[1];while(p->son[0])p=p->son[0];return p;}
while(p->fa&&p->fa->son[1]==p) p=p->fa;
return p->fa;
}
Treap *ano(int x){
if(x<=0||x>rt->sz)return NULL;
Treap *p=rt;
while(p){
if(p->son[0]&&x<=p->son[0]->sz)p=p->son[0];
else if(x<=(p->son[0]?p->son[0]->sz:0)+p->cnt)return p;
else x-=(p->son[0]?p->son[0]->sz:0)+p->cnt,p=p->son[1];
}return p;
}